二叉树的前序、中序、后序、层序遍历

参考内容：

五分钟让你彻底理解二叉树的非递归遍历

Python实现二叉树的非递归遍历

二叉树遍历——深度优先（前中后序）+广度优先（层序遍历）

构造二叉树

定义二叉树结构如下

struct node
{
    int data;
    node *left;
    node *right;
};

构造如下形态二叉树

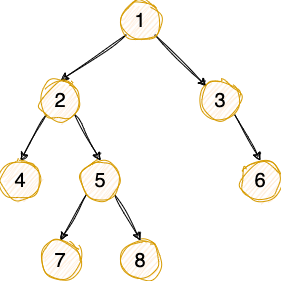
node *init_tree()
{
    node *node1 = (node *)malloc(sizeof(node));
    node *node2 = (node *)malloc(sizeof(node));
    node *node3 = (node *)malloc(sizeof(node));
    node *node4 = (node *)malloc(sizeof(node));
    node *node5 = (node *)malloc(sizeof(node));
    node *node6 = (node *)malloc(sizeof(node));
    node *node7 = (node *)malloc(sizeof(node));
    node *node8 = (node *)malloc(sizeof(node));
    
    node1->data = 1;
    node2->data = 2;
    node3->data = 3;
    node4->data = 4;
    node5->data = 5;
    node6->data = 6;
    node7->data = 7;
    node8->data = 8;

    node1->left = node2;
    node1->right = node3;
    
    node2->left = node4;
    node2->right = node5;
    
    node3->right = node6;
    
    node5->left = node7;
    node5->right= node8;

    return node1;
}

前序遍历（递归）

前序遍历顺序为根左右。要遍历整个二叉树我们就需要遍历二叉树的每一个子树，对于任何一个子树它的遍历方式均为根左右顺序遍历。即所有子问题均与父问题除规模大小不同外，其余均相同。所以可以采用递归方式实现前序遍历。

// 前序遍历 根左右
void pre_order_traversal(node *root)
{
    if(root) {
        cout<<root->data<<" ";
        pre_order_traversal(root->left);
        pre_order_traversal(root->right);
    }
}

遍历结果为：1 2 4 5 7 8 3 6

中序遍历（递归）

中序遍历顺序为左根右。其与前序遍历仅顺序不同，其余均相同。

// 中序遍历 左根右
void in_order_traversal(node *root)
{
    if(root) {
        in_order_traversal(root->left);
        cout<<root->data<<" ";
        in_order_traversal(root->right);
    }
}

遍历结果为：4 2 7 5 8 1 3 6

后序遍历（递归）

后序遍历顺序为左右根。其与前序、中序遍历仅顺序不同，其余均相同。

// 后序遍历 左右根
void post_order_traversal(node *root)
{
    if(root) {
        post_order_traversal(root->left);
        post_order_traversal(root->right);
        cout<<root->data<<" ";
    }
}

遍历结果为：4 7 8 5 2 6 3 1

前序遍历方法一（非递归）

因为递归实际上是由系统帮我们进行压栈，所以理论上所有递归算法都可以改为循环+栈实现，那么我们先照着上述前序遍历的样子修改为循环+栈的形态。需要注意的是由于栈先进后出的特性，为了保证左孩子在右孩子前被访问，所以应该先右孩子入栈，再左孩子入栈。

// 前序遍历 根左右
void pre_order_traversal(node *root)
{
    stack<node *> s;
    s.push(root);

    while(!s.empty()) {

        node *cur = s.top();
        s.pop();

        if(cur) {
            cout<<cur->data<<" ";
            s.push(cur->right);
            s.push(cur->left);
        }
    }
}

遍历结果为：1 2 4 5 7 8 3 6

前序遍历方法二（非递归）

现在我们换一种思路来实现前序非递归遍历，仔细观察前序遍历的递归调用过程。

先把从根结点开始的所有左子树放入栈中；
弹出栈顶元素
如果栈顶元素有右子树，那么右子树入栈
重复上述过程直到栈为空

因此我们可以写出遍历代码

// 前序遍历 根左右
void pre_order_traversal(node *root)
{
    stack<node *> s;
    node *cur = root;

    while(cur || !s.empty()) {
        // 将左子树全部入栈
        while(cur) {
            cout<<cur->data<<" ";
            s.push(cur);
            cur = cur->left;
        }

        if(!s.empty()) {
            cur = s.top();
            s.pop();
            cur = cur->right;
        }
    }
}

遍历结果为：1 2 4 5 7 8 3 6

中序遍历（非递归）

有了前面的基础，我们再来考虑中序遍历，会发现中序遍历与前序遍历只是打印结点的位置不一样。前序遍历是在结点入栈时打印，中序遍历只需要替换为在结点出栈时打印即可。

// 中序遍历 左根右
void in_order_traversal(node *root)
{
    stack<node *> s;
    node *cur = root;

    while(cur || !s.empty()) {
        // 将左子树全部入栈
        while(cur) {
            s.push(cur);
            cur = cur->left;
        }

        if(!s.empty()) {
            cur = s.top();
            cout<<cur->data<<" ";
            s.pop();
            cur = cur->right;
        }
    }
}

遍历结果为：4 2 7 5 8 1 3 6

后序遍历方法一（非递归）

后序遍历相对来说显得更加复杂了。在前序和中序遍历中，只要左子树处理完毕实际上栈顶元素就可以出栈了，但后序遍历需要把左子树和右子树都处理完毕才能出栈，显然我们需要某种方法记录遍历的过程。

实际上我们只需要记录下遍历的前一个结点就能解决问题，因为通过前一个结点我们可以做如下判断：

如果前一个结点是当前结点的右子树，那么说明右子树已经遍历完毕可以出栈了
如果前一个结点是当前结点的左子树而且当前结点没有右子树，那么说明可以出栈了
如果当前结点即没有左子树也没有右子树，即为叶子结点，那么说明可以出栈了

若不属于上述情况，则依次将当前结点的右孩子和做孩子入栈，这样就能保证每次取栈顶元素时，左孩子都在右孩子前面被访问，左孩子和右孩子都在父结点前面被访问。

// 后序遍历 左右根
void post_order_traversal(node *root)
{
    stack<node *> s;
    node *pre = NULL;
    node *cur = root;

    s.push(cur);

    while(!s.empty()) {
        cur = s.top();
        // 叶子结点
        if((!cur->left && !cur->right) // 叶子结点
        || pre == cur->right // 前一个结点为当前结点右子树
        || (pre == cur->left && !cur->right)) { // 前一个结点为当前结点左子树，且没有右子树
            cout<<cur->data<<" ";
            pre = cur;
            s.pop();
        } else {
            if(cur->right)
                s.push(cur->right);

            if(cur->left)
                s.push(cur->left);
        }
    }
}

遍历结果为：4 7 8 5 2 6 3 1

后序遍历方法二（非递归）

后序遍历的顺序是左右根，如果把这个顺序倒过来就是根右左，是不是发现和前序遍历很像？那么我只需要按照根右左的方式遍历完，然后将遍历结果掉一个个儿就可以，而栈就具备掉个儿的功能，因此可写出如下代码。

// 后序遍历 左右根
void post_order_traversal(node *root)
{
    stack<node *> s;
    stack<int> ans;
    node *cur = root;

    while(cur || !s.empty()) {
        // 将左子树全部入栈
        while(cur) {
            ans.push(cur->data);
            s.push(cur);
            cur = cur->right;
        }

        if(!s.empty()) {
            cur = s.top();
            s.pop();
            cur = cur->left;
        }
    }

    while(!ans.empty()) {
        cout<<ans.top()<<" ";
        ans.pop();
    }
}

遍历结果为：4 7 8 5 2 6 3 1

层序遍历

层序遍历即广度优先遍历，使用队列即可实现。

// 层序遍历
void breadth_first_order_traversal(node *root)
{
    queue<node *> q;
    q.push(root);
	while(!q.empty()){
		node *cur = q.front();
		q.pop();
		if(cur){
			cout<<cur->data<<" ";
			q.push(cur->left);
			q.push(cur->right);
		}
	}
}

遍历结果为：1 2 3 4 5 6 7 8

Guanngxu