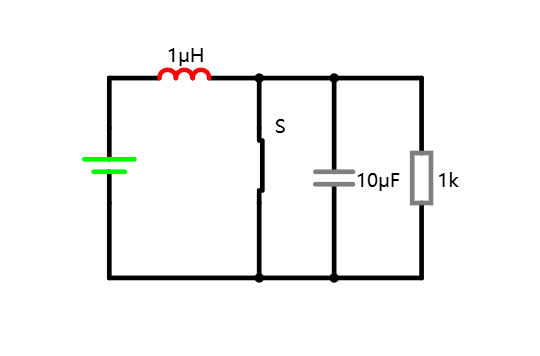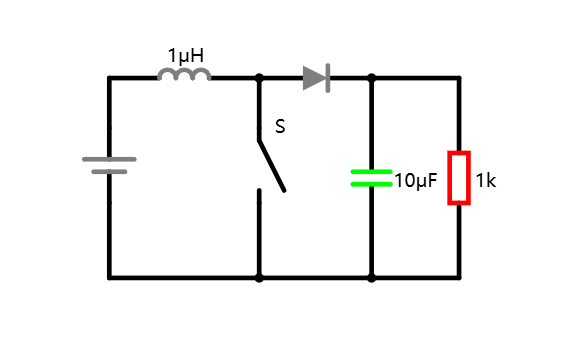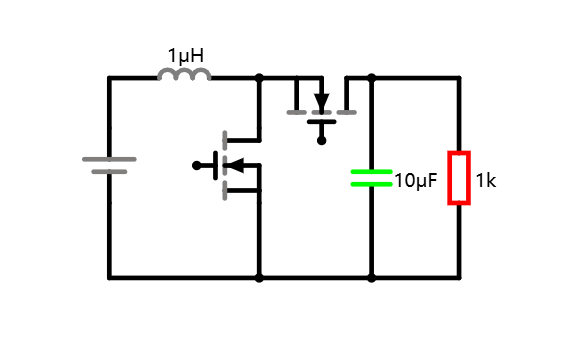参考内容：

boost升压，电感电压和输入电压叠加、实现升压

电力电子技术 05 DC-DC变换器

手撕Boost！Boost公式推导及实验验证

Boost 电路构建

我们先复习一下 BUCK 电路的基础知识。BUCK 电路是一个降压结构，在不考虑电路的损耗时，输入功率 Pin 与输出功率 Pout 是一致的。电压降低，那么电流就必然升高，因此我们可以说 BUCK 是一个降压、升流的电路。

在不考虑使用变压器的情况下，如何构造一个升压结构呢？其实换个角度想构造升压电路，其实就是构造一个降流电路出来。那么如何构造降流电路呢？

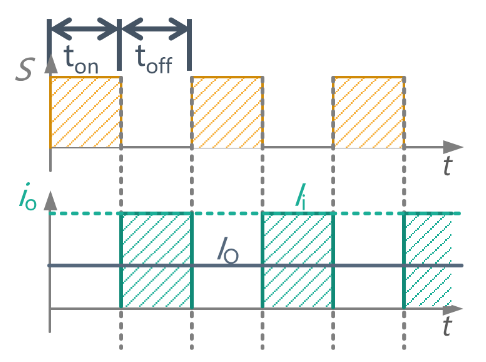
参考 BUCK 降压的原理，我们使用同样的方式对电流进行处理，即将 BUCK 电路进行改造来完成这个降流工作。下面是一个电流源、开关和负载构成的电路，当开关 S 闭合时，电流不流向负载；当开关 S 打开时，电流即流向负载。

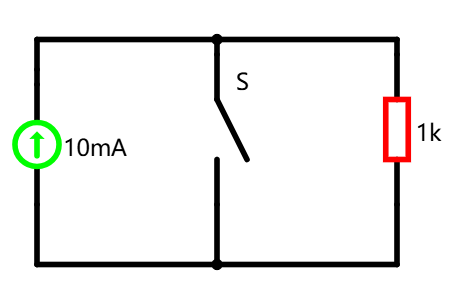
此时负载所获得的电流是一个方波，大致是下面这个样子的。可以发现与 BUCK 电路很像，我们只需要控制开关 S 的闭合时间，就可以控制流向负载的总电流。根据波形图可以确定，流向负载的电流一定小于输入电流，当开关打开时电流才流向负载。设置占空比为 D，则 Io=(1−D)IiI_{o}=(1-D)I_{i}，根据 VoIo=ViIiV_{o}I_{o}=V_{i}I_{i}，那么即有 Vo=11−DViV_{o}=\frac{1}{1-D}V _{i}

我们目前的电路还是过于理想化了，我们平时见到的都是电压源，基本没有见过电流源的场景。那么如何利用电压源做出来电流源呢？考虑到电感可以阻碍电路的变化，一个电压源串联一个电感我们可以将之近似认为是一个电流源。

回想一下前面的波形，负载所获得的电流波动太剧烈了，势必会影响电压的剧烈抖动。与 BUCK 电路的思维一致，我们还是可以用电容来进行稳压。

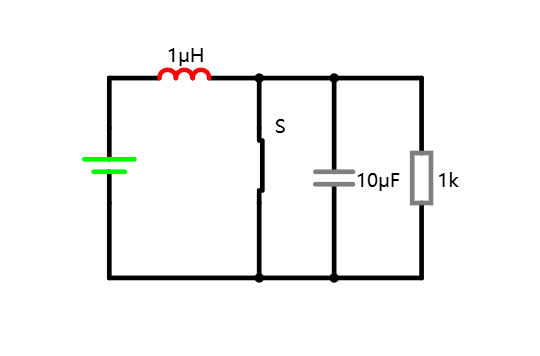
在负载端添加输出电容后，电压得以被稳定，但是考虑一下此时开关 S 闭合时是什么情况？直接将电容短路了，如何解决电容被短路的问题呢？发现当只有当 S 闭合时才会有电容短路的问题，S 打开时电流从电源端流向负载并给电容充电。我们可以通过添加一个二极管来防止 S 闭合时电容短路。

当然，也可以把二极管换成另一个开关，只要保证 S 打开时二极管位置闭合，S 闭合时二极管位置打开即可。

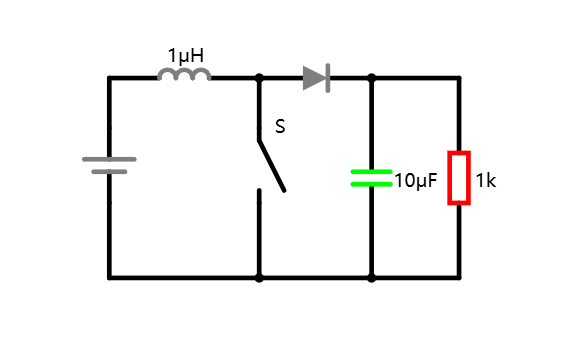
考虑到机械开关容易磨损、使用寿命短、有机械惯性（转换频率低）的问题，我们需要将机械开关换成转换频率高的半导体器件，此处我们选择 NMOS 管来替代开关。同时二极管起到的是一个开关的作用。而且考虑到电流从二极管流过期间，二极管两端的压降恒定为导通电压 0.7V，二极管所消耗的能量较大。因此我们也可以把二极管换为导通电阻更小的 NMOS 管。

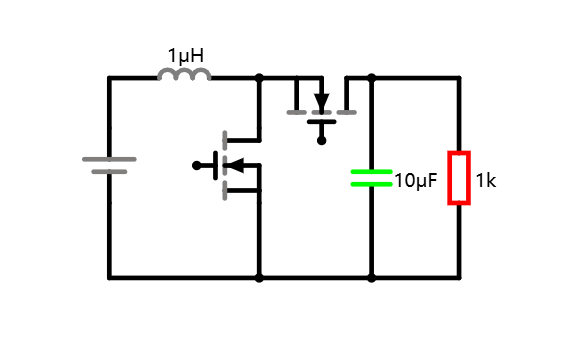
为了提高 Boost 电路的稳定性，防止由于输入纹波带来异常，我们在 Boost 电路的输入端并联一个电容，用于滤除输入电压的纹波。

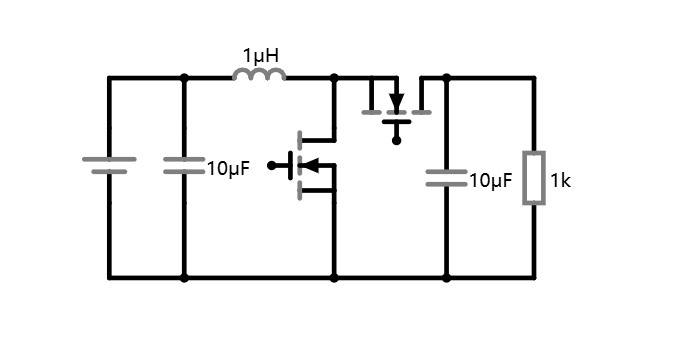
至此我们即构建了一个标准的同步 Boost 电路。回过头再来看看，我们利用储能元件从输入电源获得能量得到一个电压，并将这个电压与输入电压进行串联，以此来实现了升压的效果。电容和电感是两种常见的储能元件，使用电感或电容均可以达到升压目的。

比如 BUCK 电路中若上管为 NMOS，则需要添加 boot 电容实现升压才能打开 NMOS 管。原因在于 NMOS 导通条件为 VGS 大于 Vth，而 BUCK 电路中的 NMOS 上管 S 电压最低为 Vin，因此需要 boot 电容进行升压。

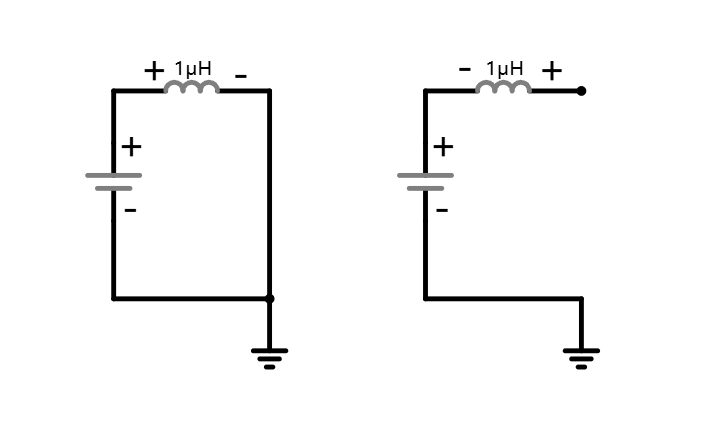
我们在 Boost 电路中使用电感来实现升压升压的功能。当电感与负载断开并接地时，电感激磁并将能量存储在电感中。当电感和输入电压断开后，由于电感电流不能突变：Vin=LdidtV_{in} =L\frac{di}{dt}，电感中变化的电流产生感应电压，感应电压与输入电压串联达到了升压目的。

稳态分析

我们所说的稳态分析，是指输入输出电压都是稳定不变的前提下进行的分析。我们将一些已知条件列出来：

  • 输入电压：ViV_{i}
  • 输出电压：VoV_{o}
  • 负载电阻：RR
  • 开关频率：ff

伏秒平衡

计算的基本原理就是电容和电感的充放电，根据前文所说的 Vo=11−DViV_{o}=\frac{1}{1-D}V _{i}，可以知道输出电压肯定大于输入电压。

在下管导通上管截止时，电感两端电压是 ViV_{i}；在下管截止上管导通时，电感右侧的电压为 VoV_{o}，左侧为电源输入 ViV_{i}，所以电感两端电压为 Vo−ViV_{o}-V_{i}。

整个电路处于稳定状态，负载电流恒定，那么在一个周期内，电感电流增加的量肯定等于电感电流减小的量，即充了多少电就要放多少电，不然负载的电流或电压将会发生变化。

前文已有didt=UL\frac{\mathrm{d} i}{\mathrm{d} t} =\frac{{U}}{L}，而 LL 恒定，那么电感电流的变化速度即与电压成正比关系，即电感电流上升（下降）的斜率与电压成正比关系。而电感电流上升和下降的高度相同，那么上升时间和下降时间就自然构成反比关系。

TonToff=Vo−ViVi\frac{T_{on} }{T_{off} } = \frac{V_{o}-V_{i}}{V_{i}}，将其进行简单变换即可得到闻名江湖的伏秒平衡法则。

TonVi=Toff(Vo−Vi)T_{on}V_{i} = T_{off}(V_{o}-V_{i})

占空比

已知 T=Ton+Toff=1fT=T_{on}+T_{off}=\frac{1}{f}，结合伏秒平衡法则可以计算出：

开通时间：Ton=Vo−ViVo∙1fT_{on} = \frac{V_{o}-V_{i}}{V_{o}} \bullet \frac{1}{f}

关断时间：Toff=ViVo∙1fT_{off} = \frac{V_{i}}{V_{o}} \bullet \frac{1}{f}

占空比：D=TonT=Vo−ViVoD = \frac{T_{on}}{T}=\frac{V_{o}-V_{i}}{V_{o}}

通过计算可以发现，占空比与电感没有关系，与负载电流大小也没有关系，只和输入输出电压有联系。

纹波电流

上文计算电感电流斜率时已经能确定电流波形是个三角波，纹波电流等于在下管导通时电感电流的增大值，也等于在下管截止时电感电流减小的值，计算任意一个即可得到纹波电流。我们以下管导通时增大的电感电流计算。

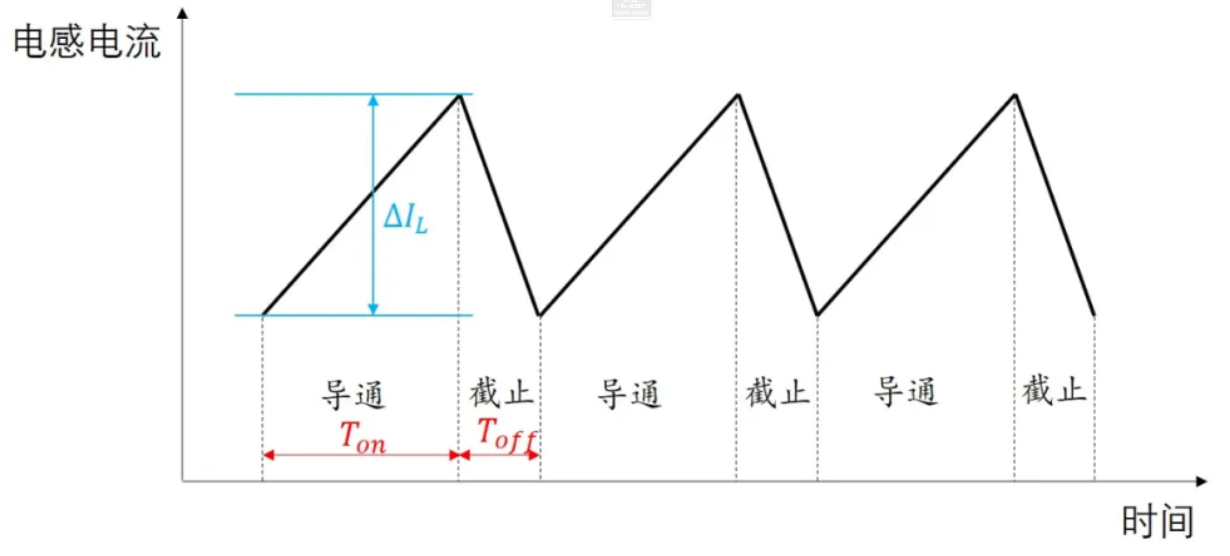
下管导通时电感两端电压为 ViV_{i}，导通时间为 Ton=Vo−ViVo∙1fT_{on} = \frac{V_{o}-V_{i}}{V_{o}} \bullet \frac{1}{f}，根据 U=LdidtU=L\frac{di}{dt} 有：

△IL=di\triangle I_{L} =di

=Ton∙UL=T_{on}\bullet \frac{U}{L}

=Vo−ViVo∙ViL∙1f=\frac{V_{o}-V_{i}}{V_{o}} \bullet \frac{V_{i}}{L} \bullet \frac{1}{f}

=(Vo−Vi)ViVoLf=\frac{(V_{o}-V_{i})V_{i}}{V_{o}Lf}

根据理论计算可以发现，电感电流的纹波和负载电流的大小没有关系。同时电感的感值会影响纹波电流的大小，因此电感的选择是系统一个很重要的参数。

功率电感选择

在系统稳态时，输出端电容是不耗电的，电压也不会有变化，所以输出电容上面流过的平均电流为 0。负载的所有电流都从上管而来，因此流过上管的平均电流也是 IoI_{o}。输入功率等于输出功率，输入电流等于流过电感的电流，即有：

ViIL=VoIoV_{i}I_{L}=V_{o}I_{o}

IL=VoIoViI_{L}=\frac{V_{o}I_{o}}{V_{i}}

计算电感峰值电流可以得到：

ILP=Io+△IL2I_{LP} =I_{o}+\frac{\triangle I_{L}}{2}

=IL+Vo−Vi2Vo∙ViL∙1f=I_{L}+\frac{V_{o}-V_{i}}{2V_{o}} \bullet \frac{V_{i}}{L} \bullet \frac{1}{f}

=VoIoVi+Vo−Vi2Vo∙ViL∙1f=\frac{V_{o}I_{o}}{V_{i}}+\frac{V_{o}-V_{i}}{2V_{o}} \bullet \frac{V_{i}}{L} \bullet \frac{1}{f}

在选择功率电感时，电感的饱和电流就必须要大于这个ILPI_{LP}，并且需要留有一定的裕量。实际应用时电感的纹波电流应是平均电流的 30%30\% 至 50%50\% 为宜，我们将这个参数称之为电流纹波率 r，关于电流纹波率为什么选择 0.3 至 0.5，可以查看为何 r 为 0.3～0.5。根据电流纹波率范围就可以计算出电感值的范围：

△IL=Vo−ViVo∙ViL∙1f\triangle I_{L} =\frac{V_{o}-V_{i}}{V_{o}} \bullet \frac{V_{i}}{L} \bullet \frac{1}{f}

L=Vo−ViVo∙Vi△IL∙1fL =\frac{V_{o}-V_{i}}{V_{o}} \bullet \frac{V_{i}}{\triangle I_{L}} \bullet \frac{1}{f}

=Vo−ViVo∙Vi(0.3至0.5)Ii∙1f=\frac{V_{o}-V_{i}}{V_{o}} \bullet \frac{V_{i}}{(0.3至0.5) I_{i}} \bullet \frac{1}{f}

=(Vo−Vi)Vi(0.3至0.5)IiVof=\frac{(V_{o}-V_{i})V_{i}}{(0.3至0.5) I_{i}V_{o}f}

输入纹波

输入电压纹波就是输入电容上面电压的变化，这个变化可以分为两部分。一部分为电容充放电所导致的电压变化 UqU_{q}，另一部分为电流流过电容 ESRESR 导致的压降 UesrU_{esr}。即 △Vi=Uq+User\triangle V_{i} = U_{q} + U_{ser}。

我们来看输入节点，这个节点的电流有三个，一个是来自电源输入的，在一个周期内我们看作是恒定的。另外两个节点是电容和电感。根据基尔霍夫电流定律，节点电流和为 0，并且电源输入的电流恒定，那么电感电流的变化量必然等于电容电流的变化量，因为最终三者的和为 0。

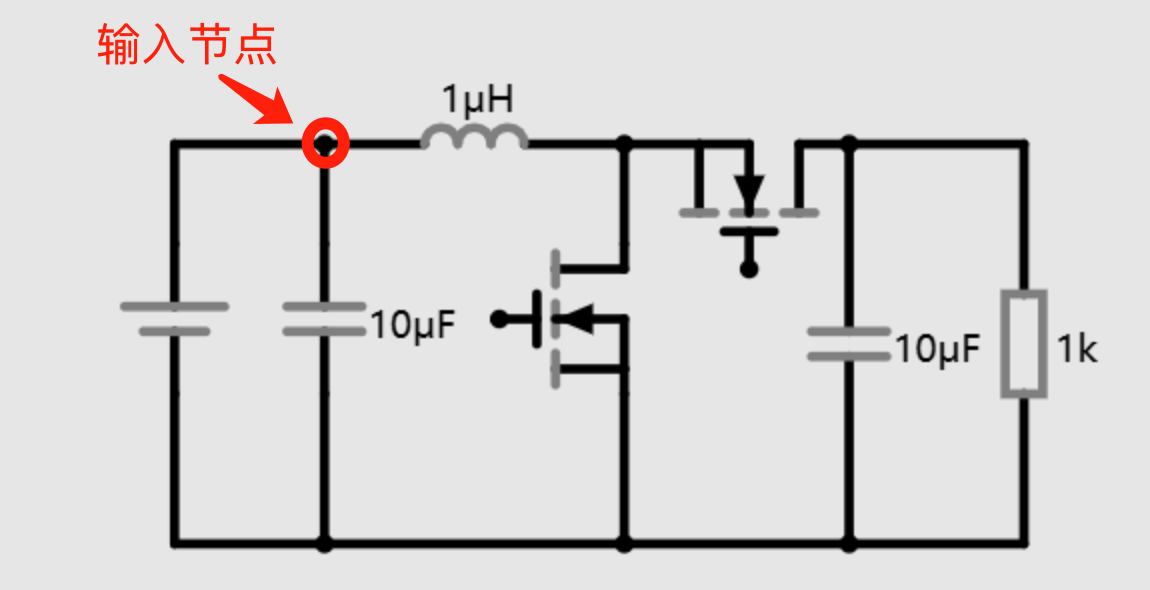
节点电流和为 0，那么输入电容的电流变化就是功率电感的电流变化。我们画出三者的电流波形。电容电流大于 0 时，电容在充电，电容电流小于 0 时，电容在放电。并且电容充电和放电时间长度是一样的，都是周期的一半。

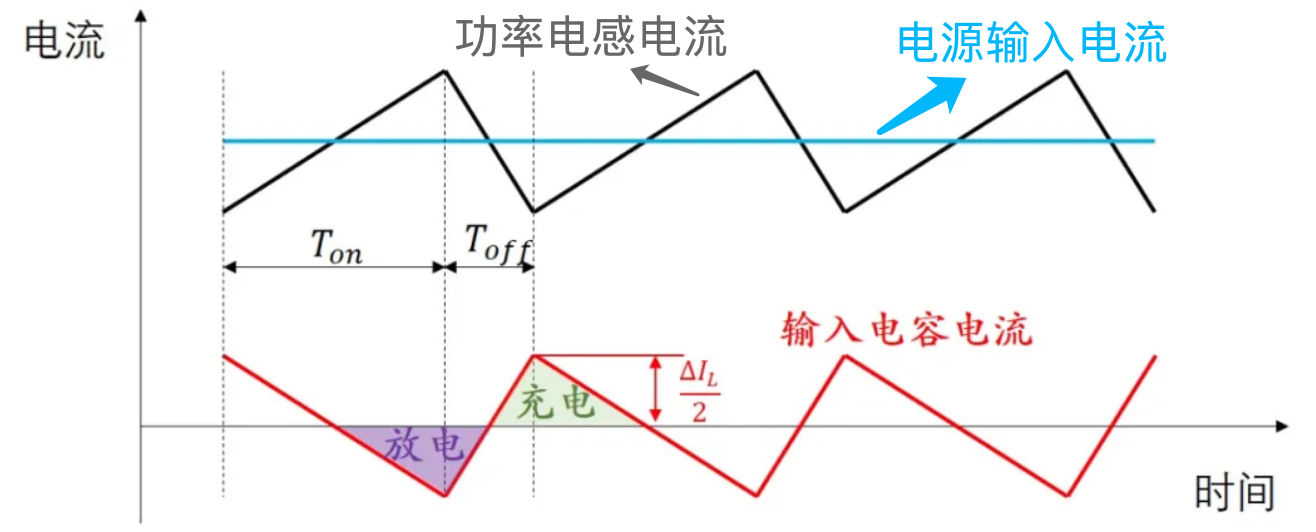
需要注意的是充电与放电的切换的时刻并不是开关导通与断开的时候，而是在中间时刻。电容充放电的总电荷量即等于电流乘以时间，其实就是图中阴影三角形的面积。

三角形底部是时间，充电/放电时间为T2\frac{T}{2}；三角形的高为电感纹波电流的一半 △IL2\frac{\triangle I_{L}}{2}；根据三角形面积计算公式即有：

Q=CiUqQ=C_{i}U_{q}

=12∙T2∙△IL2=\frac{1}{2}\bullet \frac{T}{2}\bullet \frac{\triangle I_{L}}{2}

=12∙12f∙(Vo−Vi)ViVoLf2=\frac{1}{2}\bullet \frac{1}{2f}\bullet \frac{\frac{(V_{o}-V_{i})V_{i}}{V_{o}Lf}}{2}

=(Vo−Vi)Vi8f2VoL=\frac{(V_{o}-V_{i})V_{i}}{8f^{2} V_{o}L}

Uq=(Vo−Vi)Vi8f2VoLCiU_{q}=\frac{(V_{o}-V_{i})V_{i}}{8f^{2} V_{o}LC_{i}}

前面波形图已经知道，电容的充电电流最大是 △IL2\frac{\triangle I_{L}}{2}，放电电流最大是 −△IL2-\frac{\triangle I_{L}}{2}。那么 ESRESR 引起的总压降即为：

Uesr=△IL2∙ESR−(−△IL2∙ESR)U_{esr} = \frac{\triangle I_{L}}{2} \bullet ESR - (-\frac{\triangle I_{L}}{2} \bullet ESR)

=△IL∙ESR= \triangle I_{L}\bullet ESR

=(Vo−Vi)ViVoLf∙ESR= \frac{(V_{o}-V_{i})V_{i}}{V_{o}Lf} \bullet ESR

最终可得：

△Vi=Uq+Uesr\triangle V_{i} = U_{q} + U_{esr}

=(Vo−Vi)Vi8f2VoLCi+(Vo−Vi)ViVoLf∙ESR=\frac{(V_{o}-V_{i})V_{i}}{8f^{2} V_{o}LC_{i}} + \frac{(V_{o}-V_{i})V_{i}}{V_{o}Lf} \bullet ESR

输入电容选择

考虑到电容的实际使用情况，陶瓷电容的 ESRESR 小，容量小，所以 UqU_{q} 对纹波起决定性作用，输入纹波可近似为 UqU_{q}。若选择铝电解电容，则 ESRESR 大，容量大，UesrU_{esr} 对纹波起到决定性作用，输入纹波可以近似为 UesrU_{esr}，假设电路设计要求输入纹波不能大于 △Vi\triangle V_{i}，则有：

陶瓷电容：Ci≥(Vo−Vi)Vi8f2VoL△ViC_{i} \ge \frac{(V_{o}-V_{i})V_{i}}{8f^{2} V_{o}L \triangle V_{i}}

铝电解电容：ESR≤△ViVoLf(Vo−Vi)ViESR \le \frac{\triangle V_{i}V_{o}Lf}{(V_{o}-V_{i})V_{i}}

输出纹波

输出纹波与输入纹波同理，亦是 △Vo=Uq+Uesr\triangle V_{o} = U_{q} + U_{esr}。一个周期内电容的充电电荷必然与放电电荷量相等，我们只需要计算出其中任意一个即可。很显然计算放电电荷量更为容易，因为放电电流就是负载电流，负载电流为恒定的 Io=VoRLI_{o} = \frac{V_{o}}{R_{L}}。

Q=CoUq=IoTonQ = C_{o}U_{q}=I_{o}T_{on}

Ton=Vo−ViVo∙1fT_{on} = \frac{V_{o}-V_{i}}{V_{o}} \bullet \frac{1}{f}

Uq=IoTonCoU_{q} = \frac{I_{o}T_{on}}{C_{o}}

=Io(Vo−Vi)CoVof= \frac{I_{o}(V_{o}-V_{i})}{C_{o}V_{o}f}

在下管导通的时候，负载的电流为 IoI_{o}，完全由输出滤波电容提供，即滤波电容的放电电流也为 IoI_{o}，而且还是在导通时间里面恒定不变的。

在下管从导通切换到截止时，电感的电流已经是充到最大的，因为先前下管导通时电感一直在充电，所以切换时电感电流最大，且等于电感平均电流加上纹波电流的一半，即 IL+△IL2I_{L}+\frac{\triangle I_{L}}{2}。已经充好的电感电流会给负载供电，负载电流为 IoI_{o}。同时电感还要给输出电容进行充电，根据基尔霍夫电流定律，电容的充电电流就是电感充到最大的电流减去负载的电流，即 IL+△IL2−IoI_{L}+\frac{\triangle I_{L}}{2} - I_{o}。

在下管关断之后，电感电压反向，电感电流持续减小，负载电流恒定不变，所以输出滤波电容的电流持续减小。画出输出电容的电流波形就非常明显了。

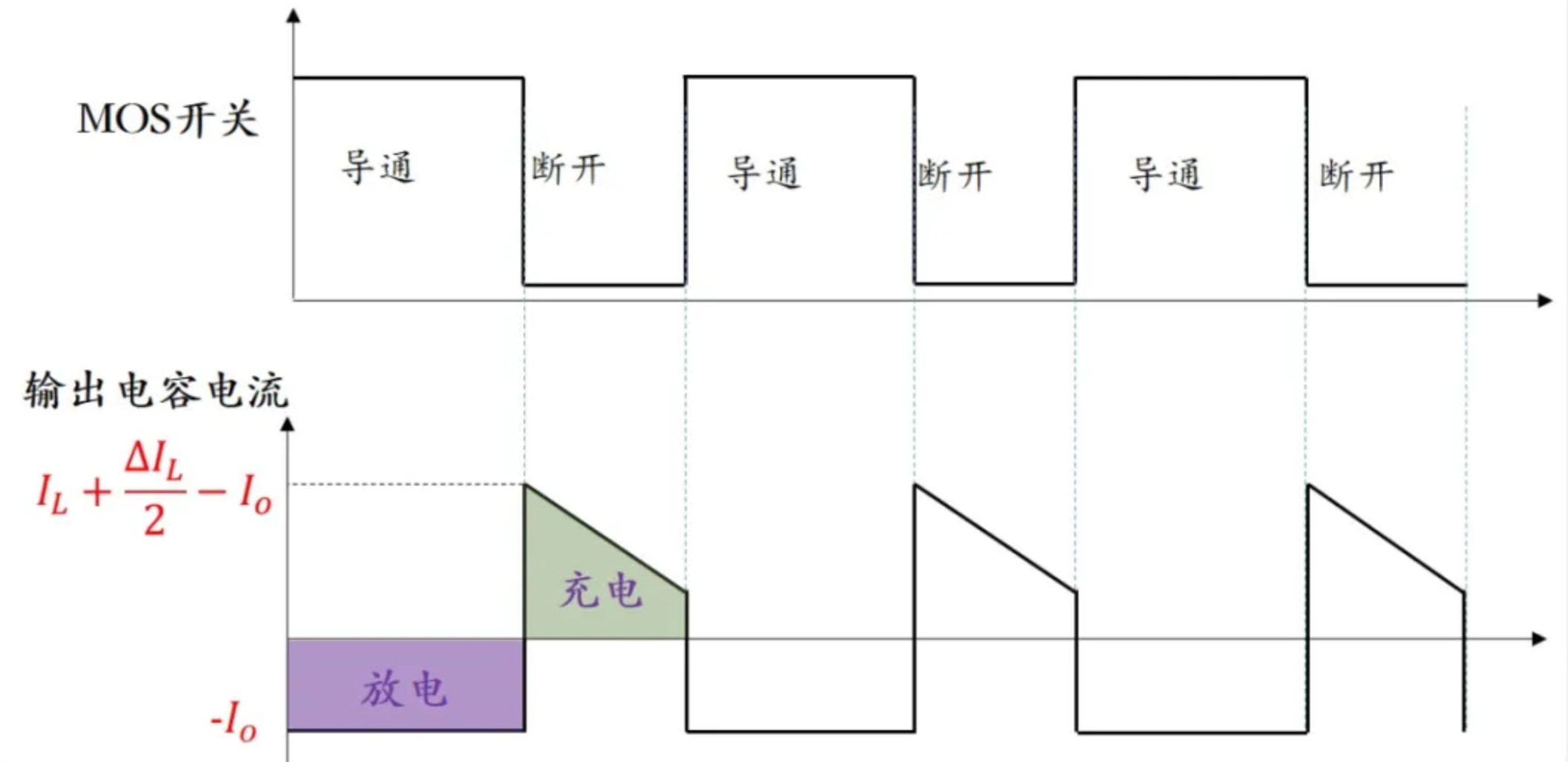
在下管导通时，ESRESR 两端的电流为 −Io-I_{o}。在下管截止时，ESRESR 两端的电流为 IL+△IL2−IoI_{L}+\frac{\triangle I_{L}}{2} - I_{o}。由此即可计算出 ESRESR 上的电压变化量。

Uesr=(IL+△IL2−Io)∙ESR−(−Io∙ESR)U_{esr} = (I_{L}+\frac{\triangle I_{L}}{2} - I_{o})\bullet ESR - (-I_{o} \bullet ESR)

=(IL+△IL2)∙ESR= (I_{L}+\frac{\triangle I_{L}}{2})\bullet ESR

=(VoIoVi+(Vo−Vi)Vi2VoLf)∙ESR= (\frac{V_{o}I_{o}}{V_{i}} + \frac{(V_{o}-V_{i})V_{i}}{2V_{o}Lf}) \bullet ESR

最终可得：

△Uo=Uq+Uesr\bigtriangleup U_{o} = U_{q} + U_{esr}

=Io(Vo−Vi)CoVof+(VoIoVi+(Vo−Vi)Vi2VoLf)∙ESR=\frac{I_{o}(V_{o}-V_{i})}{C_{o}V_{o}f} + (\frac{V_{o}I_{o}}{V_{i}} + \frac{(V_{o}-V_{i})V_{i}}{2V_{o}Lf}) \bullet ESR

输出电容选择

与输入电容选择的方式一致，考虑是容值还是 ESRESR 占主导地位，假设要求输出纹波要小于 △Vo\triangle V_{o}，则有：

陶瓷电容：Co≥Io(Vo−Vi)△VoVofC_{o} \ge \frac{I_{o}(V_{o}-V_{i})}{\triangle V_{o}V_{o}f}

铝电解电容：ESR≤△VoVoIoVi+(Vo−Vi)Vi2VoLfESR \le \frac{\triangle V_{o}}{\frac{V_{o}I_{o}}{V_{i}} + \frac{(V_{o}-V_{i})V_{i}}{2V_{o}Lf}}