参考内容:
本文首发于牛客网:题解 | #牛牛摆木棒#
题目
牛客网 NC632 牛牛摆木棒、POJ1037-A decorative fence(美丽的栅栏)
描述
有n个木棒,长度为1到n,给定了一个摆放规则。规则是这样的:对于第 i 个木棒 , && 或 && 。求满足规则的从小到大的第k个排列是什么呢。
对于两个排列 s 和 t:如果存在 j 有任意 使得 且 ,视为排列 s 小于排列 t。
示例
输入:3,3
返回值:[2,3,1]
说明:第一小的排列为:[ 1 , 3 , 2 ]
第二小的排列为:[ 2 , 1 , 3 ]
第三小的排列为:[ 2 , 3 , 1 ]
第四小的排列为:[ 3 , 1 , 2 ]
所以答案为:[ 2 , 3 , 1 ]
备注
题意
该问题让我们求:n 的字典序排列中第 k 个波浪形的排列。什么是波浪形排列呢?即对排列中任意一个数字(除开第一个和最后一个),只能 比 和 都小或者都大。比如 2 1 3和1 3 2是波浪形排列,但1 2 3就不是波浪形排列。
DFS 枚举
最容易想到的解决方案是把 n 的所有排列按字典序列出来,然后再逐一检查是否是波浪形排列,直接取出第 k 个波浪形排列即可。
我们以 3 的全排列为例画出如下树形图,非常容易的就能发现只要对这棵树进行深度优先遍历,就能够按字典序得到所有排列。但并不是所有排列都满足波浪形这个条件,所以我们每得到一个排列都需要检查该排列是否为波浪形,直到检查到第 k 个排列为止,返回该排列即可。

class Solution {
public:
// 记录当前已经有多少个波浪形排列
long long count = 0;
// 记录最后的结果
vector<int> res;
/**
*
* @param n int整型 木棒的个数
* @param k long长整型 第k个排列
* @return int整型vector
*/
vector<int> stick(int n, long long k) {
// 用于标记当前考虑的数字是否已经被选择
bool visited[25] = {false};
// 用于记录已经选了哪些数
vector<int> path;
dfs(n, 0, path, visited, k);
return res;
}
/**
*
* @param n 可选的数字范围
* @param deep 递归到第几层了
* @param path 已经选的数字
* @param visited 记录哪些数已经被选了
* @param k 是否已经到第 k 个波浪形排列了
*/
void dfs(int n, int deep, vector<int> path, bool visited[], long long k) {
// 递归层数和范围相等,说明所有的数字都考虑完了,因此得到一个排列
if(deep == n){
// 判断该排列是否为波浪形排列
bool flag = true;
for(int i = 1; i < n-1; i++){
if((path[i] > path[i-1] && path[i] < path[i+1]) ||
(path[i] < path[i-1] && path[i] > path[i+1])){
flag = false;
break;
}
}
// 是波浪形排列,则统计一次
if(flag) {
count++;
}
// 判断是否已经到第 k 个排列
if(count == k) {
// 如果返回结果还没有被赋值,则将该排列赋值给 res
// 因为我们使用的是递归,所以 count==k 会被满足多次
// 只有第一次满足时才是真正的 k 值,所以必须判断 res 是否为空
// 如果不判空,则程序记录的不是正确结果
if(res.empty()){
res = path;
}
// 到第 k 个波浪形排列了,递归返回
return ;
}
// 没有可以选择的数字了,回溯
return ;
}
// 还没有得出一个排列,则继续挑选数字组成排列
for(int i = 1; i <= n; i++) {
// 如果该数字已经被选择了,则终止本次循环
if(visited[i]){
continue;
}
// 选中当前数字加入到排列中
path.push_back(i);
visited[i] = true;
// 下一次递归所传的值不变,只有递归层数需要 +1
dfs(n, deep+1, path, visited, k);
// 回溯,需要撤销前面的操作
path.pop_back();
visited[i] = false;
}
}
};
在 C++ 的 algorithm 库中已经提供了一个全排列方法 next_permutation。按照STL文档的描述,next_permutation 函数将按字母表顺序生成给定序列的下一个较大的序列,直到整个序列为减序为止。因此我们可以偷个懒直接使用现有的函数。
class Solution {
public:
/**
*
* @param n int整型 木棒的个数
* @param k long长整型 第k个排列
* @return int整型vector
*/
vector<int> stick(int n, long long k) {
vector<int> res;
// 记录当前已经有多少个波浪形排列
long long count = 0;
// 构造初始化排列
for(int i = 1; i <= n; i++) {
res.push_back(i);
}
do {
// 判断当前排列是否为波浪形排列
bool flag = true;
for(int i = 1; i < n-1; i++) {
if((res[i] > res[i-1] && res[i] < res[i+1]) ||
(res[i] < res[i-1] && res[i] > res[i+1])){
flag = false;
break;
}
}
if(flag) {
count++;
}
if(count == k) {
break;
}
} while (next_permutation(res.begin(), res.end()));
return res;
}
};
复杂度分析
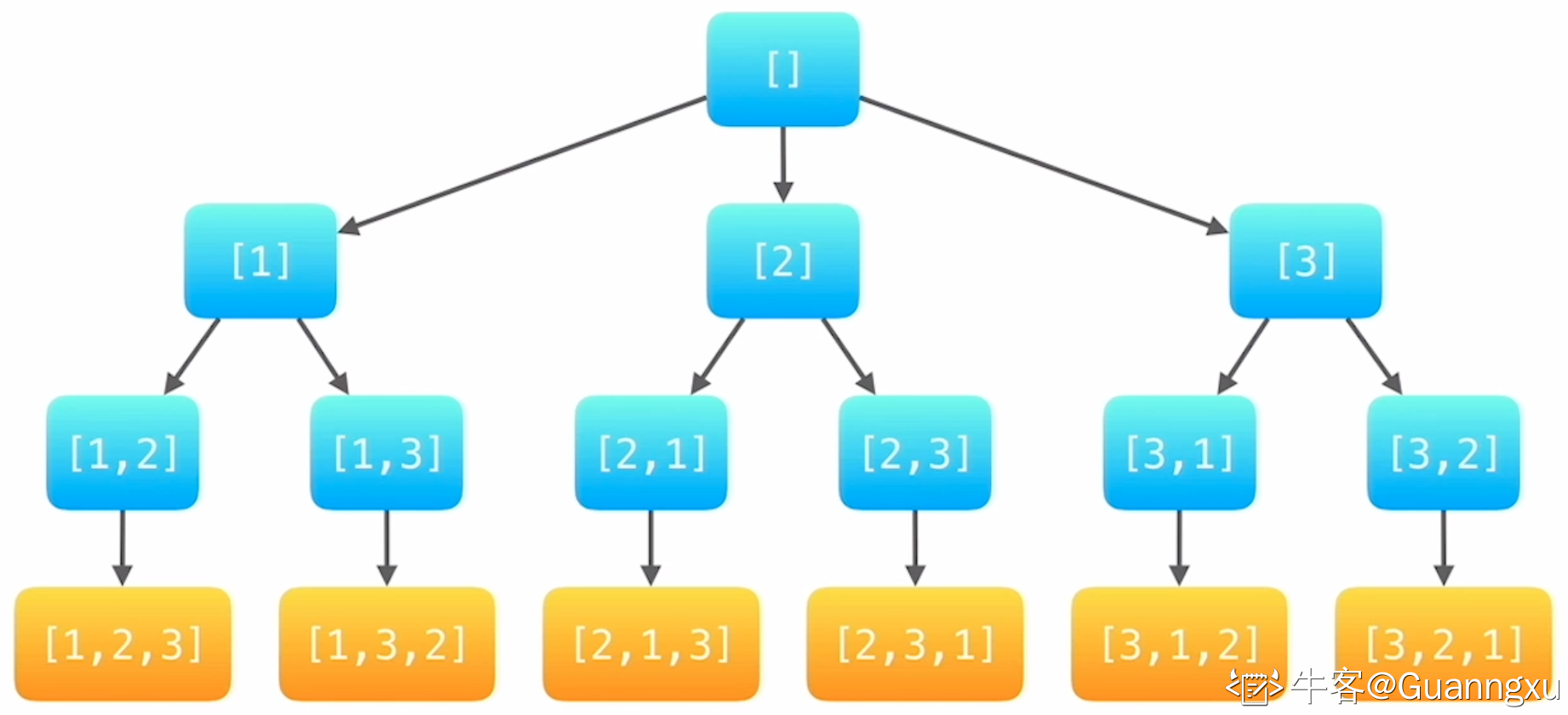
我们来看一下这个深度优先遍历的时间复杂度分析,该算法的时间复杂度主要由递归树的结点个数决定。因为程序在叶子结点和非叶子结点的行为时不一样的,所以我们先计算非叶子结点的个数,我们一层一层的去计算它。
第 1 层因为只有一个空列表,所以我们不考虑它;
第 2 层表示的意思是从 n 个数中找出 1 个数,即 ;
第 3 层表示的意思是从 n 个数中找出 2 个数,即 ;
以此类推,全部非叶子结点的总数为:
每个非叶子结点都在内部循环了 n 次,所以非叶子结点的时间复杂度为 ,去除系数后得到 。
最后一层叶子结点的个数就是 个,但是我们对每个叶子结点都做了一次判断,因此叶子结点的时间复杂度依然是 。
该问题的 k 控制了遍历的次数,最好情况即 ,最差即 ,平均一下也不过只加了个系数,因此总的时间复杂度为 。
递归树的深度为 n,需要 的空间;程序运行过程中保存了问题的最终答案,需要 的空间,总共需要 的空间,因此该算法的空间复杂度为 。
动态规划
上述算法在运行过程中会超时,究其原因就是不论测试数据要求我们求第几个波浪形排列,我们都老老实实的从第一个开始数,当数据比较大时就会出现超时的情况。那么有没有办法能够减少一些不必要的过程呢?比如测试数据要求第 100 个波浪形排列,很明显前面 80 个排列肯定不满足情况,我们能否舍弃一部分搜索直接从第 80 个甚至第 90 个开始呢?
我们先不考虑波浪形排列这个条件,如果是求第 k 个全排列的话是非常容易就能算出来的。还是以1 2 3的全排列为例,假设现在要求第 5 个全排列,可以发现只要第一个数确定了,排列数就由剩下数的排列方案决定,以1打头的排列有两个,以2打头的排列也有两个,而现在要求的是第 5 个排列,所以肯定不是以1或2打头的,这样我们就能直接跳过大部分不合法的排列,节省了时间。
仔细想想发现理想是比较丰满,上述方法的问题在于无法确定前面跳过的那部分里面究竟有多少个波浪形排列,因此这种直接计算的方法行不通。但是这个思想我们是可以借用一下的,那我们把一部分数据计算出来,尝试一下能不能找到规律。
当 n 为 1 时,总共有 1 个波浪形排列,1 打头的有 1 个;
当 n 为 2 时,总共有 2 个波浪形排列,1 打头的有 1 个;
当 n 为 3 时,总共有 4 个波浪形排列,1 打头的有 1 个;
当 n 为 4 时,总共有 10 个波浪形排列,1 打头的有 2 个;
当 n 为 5 时,总共有 32 个波浪形排列,1 打头的有 5 个;
当 n 为 6 时,总共有 122 个波浪形排列,1 打头的有 16 个;
列出来了 6 组数据都没有发现规律,这种方式基本得战略性放弃了。我们设置 A[i] 为 i 根木棒所组成的合法方案数,列数据找规律其实就是尝试找到 A[i] 和 A[i-1] 的规律,比如选定了某根木棒 x 作为第 1 根木棒的情况下,则剩下 i-1 根木棒的合法方案数为 A[i-1]。问题在于并不是这 A[i-1] 中每一种方案都能和 x 形成一种新的合法方案。
我们把第 1 根木棒比第 2 根木棒长的方案称为 W 方案,第 1 根木棒比第 2 根木棒短的方案称为 M 方案。A[i-1] 中方案中只有第 1 根木棒比 x 要长的 W 方案,以及第 1 根木棒比 x 要短的 M 方案,才能进行组合构成 A[i] 中的合法方案。
因此我们可以设A[i] = 0,先枚举 x,然后针对每一个 x 枚举它后面那根木棒 y,如果y > x(y < x同理)则有:A[i] = A[i] + 以 y 打头的 W 方案数,但是以 y 打头的 W 方案数,又和 y 的长短有关,因此只能继续将描述方式继续细化了。
设 B[i][k] 是 A[i] 中以第 k 短的木棒打头的方案数,则有:
公式中(W) 和 (M) 分别表示 W 方案和 M 方案,发现还是无法找出推导关系。设 C[i][k][0] 为 B[i][k] 中的 W 方案数,C[i][k][1] 为 B[i][k] 中的 M 方案数那么则有:
至此状态转移方程就出来了,初始条件为:C[1][1][0]=C[1][1][1] = 1,下面就可以开始写代码了。
class Solution {
public:
/**
*
* @param n int整型 木棒的个数
* @param k long长整型 第k个排列
* @return int整型vector
*/
vector<int> stick(int n, long long s) {
long long dp[21][21][2];
memset(dp,0,sizeof(dp));
dp[1][1][0] = dp[1][1][1] = 1;
for (int i = 2; i <= n; i++){
// 枚举第一根木棒的长度
for (int k = 1; k <= i; k++){
// W 方案枚举第二根木棒的长度
for (int m = k; m < i; m++){
dp[i][k][0] += dp[i-1][m][1];
}
// M 方案枚举第二根木棒的长度
for (int m = 1; m <= k-1; m++){
dp[i][k][1] += dp[i-1][m][0];
}
}
}
// 标记是否已经使用
bool visited[21] = {false};
// 保存结果的排列
int a[21];
// 逐一确定第 i 位
for(int i = 1; i <= n; i++) {
int k = 0;
// 假设第 i 放 j
for(int j=1;j<=n;j++) {
long long tmp = s;
// 已经使用过的数不能再使用了
if(!visited[j]) {
// j 是没有使用过的木棒中第 k 短的
k++;
if(i == 1) {
// 确定第一根木棒的长度
tmp -= dp[n][k][0] + dp[n][k][1];
} else if(j < a[i-1] && (i==2 || a[i-2]<a[i-1])) {
// W 类型
tmp -= dp[n-i+1][k][0];
} else if(j > a[i-1] && (i==2 || a[i-2]>a[i-1])) {
// M 类型
tmp -= dp[n-i+1][k][1];
}
if(tmp <= 0) {
visited[j]=true;
a[i]=j; // 第 i 位为 j
break;
}
}
s = tmp;
}
}
// 将结果转换为指定格式
vector<int> res;
for(int i = 1; i <= n; i++) {
res.push_back(a[i]);
}
return res;
}
};
复杂度分析
最开始初始化dp数组时用了 的时间,随后填写dp数组花的时间为 ,计算最终答案的时间为 ,将结果转为指定格式的时间为 ,所以该算法的时间复杂度为 。
dp数组占用了 的空间,标记数组visited、保存结果的数组a,以及最终转换为指定格式的path向量,各占用了 的空间,取最大值即该算法的空间复杂度为 ,去掉系数得到最终空间复杂度 。