动态规划实例——01 背包详解

题目描述

有 n 件物品，每件物品有一个重量和一个价值，分别记为 w1，w2，…，wn 和 c1，c2，…，cn。现在有一个背包，其容量为 wk，要从 n 件物品种任取若干件。要求：（1）重量之和小于或等于 wk；（2）价值之和最大。

输入：

共 3 行，第一行 2 个整数，表示 n 和 wk；第二行 n 个整数表示每一个物品的重量，第三行 n 个整数表示每一个物品的价值。

输出：

一行一个整数，表示符合背包容量的最大价值。

样例：

8 200
79 58 86 11 28 62 15 68
83 14 54 79 72 52 48 62

暴力枚举

我们以只有 A、B、C 三件物品的情况为例，对于每一个物品都存在拿和不拿两种情况。以0表示不拿当前物品，以1表示拿当前物品，可以有如下分析结果。

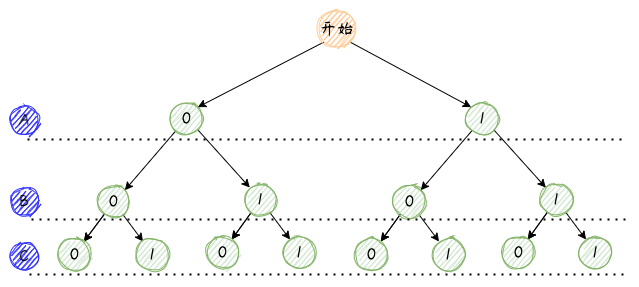
可能上面的图看起来不够清晰，我们从左至右逐一列举出来观察，一眼就可以看出来规律。其实就是十进制的 0、1、2、3、4、......可枚举的最大值即 2ⁿ-1。

根据上面的分析，我们可以写出如下代码。

#include<bits/stdc++.h>
using namespace std;

int main()
{
	int n, wk;
	int w[10000], c[10000];
	cin>>n>>wk;
	for(int i = 0; i < n; i++){
		cin>>w[i];
	}
	for(int i = 0; i < n; i++){
		cin>>c[i];
	}

	int ans = 0;
    int max_val = 1 << n;
    // 逐一枚举
	for(int i = 0; i < max_val; i++){
		int ww = 0, cc = 0;
		int index = 0;
		// 转二进制
		int cur = i;
		while(cur){
			int bit = cur % 2;
            // 若拿第 index 个物品，则累加其重量和价值
			if(bit){
				ww += w[index];
				cc += c[index];
			}
			cur = cur >> 1;
			index++;
		}
		//计算最大值
		if(ww <= wk && ans < cc){
			ans = cc;
		}
	}
	//输出最大值
	cout<<ans<<endl;
}

递归求解

我们把背包容量为wk，有n个物品可以选择的问题表示为slove(wk, n)。那么在背包剩余容量可以装下第 n 个物品时，该问题可以表示为求如下两个问题的最大值

选第 n 个物品：c[n-1] + slove(wk-w[n-1], n-1)
不选第 n 个物品：slove(wk, n-1)

在背包剩余容量无法装下第 n 个物品时，问题直接变为

不选第 n 个物品：slove(wk, n-1)

可以发现上述三个子问题可以继续向下拆分为规模更小，但类型一致的子子问题。于是可以写出如下递归求解代码。

#include<bits/stdc++.h>
using namespace std;

int w[30]={0}, c[30]={0};

// wk 背包剩余重量
// ch 可选项
int slove(int wk, int ch)
{
	if(wk <= 0 || ch <= 0){
		return 0;
	}
	
    // 若背包剩余容量无法装下 w[ch-1]，则直接丢弃第 ch 个物品
	if(w[ch-1] > wk){
		return slove(wk, ch-1);
	}
	
    // 若背包剩余容量能装下 w[ch-1]，则计算装和不装的最大值
	int a = c[ch-1] + slove(wk-w[ch-1],ch-1);
	int b = slove(wk, ch-1);
	return a > b ? a : b;
}

int main()
{
	int n, wk;
	cin>>n>>wk;
	
	for(int i = 0; i < n; i++){
		cin>>w[i];
	}
	for(int i = 0; i < n; i++){
		cin>>c[i];
	}
	cout<<slove(wk, n);
}

动态规划

递归在执行过程中会存在重复计算相同子问题的情况，我们可以将其改为用循环实现，即动态规划的写法。dp[i][j]的含义即为：在背包容量为i，可选物品数量为j的情况下，符合背包容量的最大值。具体代码如下所示：

#include<bits/stdc++.h>
using namespace std;

int w[30]={0}, c[30]={0};

int main()
{
	int n, wk;
	cin>>n>>wk;
	
	for(int i = 0; i < n; i++){
		cin>>w[i];
	}
	for(int i = 0; i < n; i++){
		cin>>c[i];
	}

    int dp[1000001][21] = { 0 };

    for(int i = 1; i <= wk; i++) {
        for(int j = 1; j <= n; j++) {
            // 若背包剩余容量无法装下 w[j-1]，则直接丢弃第 j 个物品
            if(w[j-1] > i) {
                dp[i][j] = dp[i][j-1];
            } else {
                // 若背包剩余容量能装下 w[j-1]，则计算装和不装的最大值
                int a = c[j-1] + dp[i-w[j-1]][j-1];
                int b = dp[i][j-1];
                dp[i][j] = a > b ? a : b;
            }
        }
    }

	cout<<dp[wk][n];
}

Guanngxu